① 定性解释
由图2.3 和(2.1)式知道,渐变光纤的折射率分布是在光纤的轴心处最大,而沿剖面径向的增加而折射率逐渐变小。采用这种分布规律是有其理论根据的。假设光纤是由许多同轴的均匀层组成,且其折射率由轴心向外逐渐变小,如图2.8 所示。
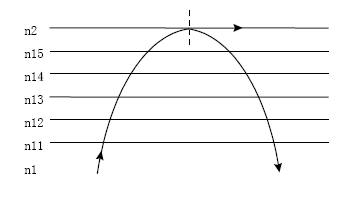
图2.8 光在渐变光纤中传播的定性解释
即n1>n11>n12>n13……>n2
由折射定律知,若n1>n2,则有θ2>θ1。这样光在每二层的分界面皆会产生折射现象。由于外层总比内层的折射率要小一些,所以每经过一个分界面,光线向轴心方向的弯曲就厉害一些,就这样一直到了纤芯与包层的分界面。而在分界面又产生全反射现象,全反射的光沿纤芯与包层的分界面向前传播,而反射光则又逐层逐层地折射回光纤纤芯。就这样完成了一个传输全过程,使光线基本上局限在纤芯内进行传播,其传播轨迹类似于由许多许多线段组成的正弦波。
② 传播轨迹
再进一步设想,如果光纤不是由一些离散的均匀层组成,而是由无穷多个同轴均匀层组成。换句话讲,光纤剖面的折射率随径向增加而连续变化,且遵从抛物线变化规律,那么光在纤芯的传播轨迹就不会呈折线状,而是连续变化形状。理论上可以证明,若渐变光纤的折射率,分布遵从(2.1)式,则光在其中的传播轨迹为:

其中
A为正弦曲线振幅,待定常数a1为纤芯半径
Δ为相对折射率差
Φ为初始相位,待定常数
于是以不同角度入射的光线族皆以正弦曲线轨迹在光纤中传播,且近似成聚焦状,如图2.9 所示。
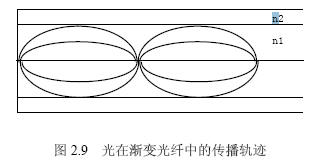
|